A C++ worker pool using thread and functional

To celebrate the fifth anniversary of the TBZ533 blog, I decided the revisit the first post. This was about a class that could be inherited to provide worker pool functionality, implemented with the pthread library and function pointers. Using a bit of modern C++, the implementation of a simple worker pool becomes much more elegant.

In the header file workerpool.hpp, we declare the WorkerPool class. The argument of the constructor is the number of workers. If the number of workers is zero, all tasks are executed serially (which can be convenient for debugging). A WorkerPool can not be copied, so we disable the copy constructor and copy assignment constructor. A Task is defined as a function that takes no arguments and returns nothing. A Task can be passed to the worker pool using the push_back() method (which name is inspired by std::list::push_back()). The final public method is the sync() method that waits for all tasks to be completed.

The private methods and members of WorkerPool are a vector of worker threads, a list of (unfinished) tasks, the worker routine, and some synchronization objects. The boolean abort_flag is used to get the workers to exit their worker routines. The count integer represents the number of unfinished tasks. Tasks are guarded by the task_mut mutex, and count by the count_mut mutex. The task_cv condition variable is used to signal that a new Task is added to the list of tasks, while the count_cv is used to signal that another task has been completed.



The source file contains the definitions of the methods of WorkerPool. The constructor initiates a number of worker threads and starts their worker_routine(). The descructor makes sure that all threads exit their worker routine and joins the threads. This means that the WorkerPool uses the RAII technique. The push_back() method evaluates the Task object if there are no workers, and otherwise adds the task to the tasks list, after increasing the count. We signal that a task has been added in case a worker is sleeping. The sync() method only returns when count == 0. Finally, the most important part of the code is the worker_routine(). When the list tasks is empty, a worker waits until a signal is given that a new tasks is added, or the abort_flag is set. In the first case, the task is executed, in the second case, the worker exits the worker_routine().

Example: drawing the Mandelbrot set in parallel

To give a nice example of how the WorkerPool should be used, I modified some code from Farouk Ounane for drawing the Mandelbrot set in C++. Each Task determines if a point in the complex plane is part of the Mandelbrot set or not. We use a closure (lambda expression) to define these tasks, and pass them to the WorkerPool. The result is shown above. To compile the C++ program with gcc, put the files workerpool.cpp, workerpool.hpp and mandelbrot.cpp in the same directory, and execute from the terminal

  g++ workerpool.cpp mandelbrot.cpp -o mandelbrot -pthread -std=c++11
  

My Matplotlib Cheatsheet (#2)

Previously, I wrote about some matplotlib methods I often use. In this post I will show two more.

Scatter plots with color for density

Scatter plots with many points can become very uninformative. A very easy solution is to color the points according to their local density. This can be done with the gaussian_kde from scipy.stats. Suppose that we want to make a scatter plot from xs and ys in subplot ax, then we just have to add two lines to color the points:

xy = numpy.vstack([xs, ys])
z = scipy.stats.gaussian_kde(xy)(xy)
ax.scatter(xs, ys, s=5, c=z)

Here's an example:

This is the code I used to make the figure, making use of inset_axes for a color bar:

Recycling bins for multiple histograms

When you want to plot multiple histograms in one plot, the width of the bins can be very different, which does not look so good. I recently found a simple method to fix this. The second value that the hist function returns specifies the boundaries of the bins used for the histogram. This value can be used directly in the next call to the hist function using the bins keyword. The following figure shows the result:

I used the following code to plot this figure:

Generalized Profiling with Stan

The probabilistic programming language Stan has built-in support for ODE models through the higher-order functions integrate_ode_rk45 and integrate_ode_bdf. Here, I will demonstrate an alternative way to implement ODE models in Stan, that has some interesting benefits. This method is called generalized profiling and has been developed by Ramsay et al. in 2007.

In a previous blog post, I used the Lotka-Volterra predator-prey model as an example for an ODE model in Stan. The model is given by the 2-dimensional system of ODEs $$ \frac{dx}{dt} = a x - b xy\,,\quad \frac{dy}{dt} = c b xy - dy $$ with initial conditions \(x(0) = x_0\) and \(y(0) = y_0\). Here, \(x\) and \(y\) represent the prey and predator "concentrations", respectively. If we choose a system size \(K\), we can generate some data \(X_i \sim \mathrm{Poisson}(K x(t_i))\) and \(Y_i \sim \mathrm{Poisson}(K y(t_i))\) at times \(0\leq t_i \leq T\). However, when we implement this model in Stan with integrate_ode_rk45, and try to estimate the parameters \(a, b, c, d, x_0, y_0\) without giving any initial guesses for these parameters, Stan will have a really hard time finding any good values. The reason for this is that for non-linear systems of ODEs the posterior density can be quite "rugged", i.e. can contain many local optima that even Stan's NUTS sampler can have a hard time navigating through. The generalized profiling method solves this problem by modifying the model in such a way that the posterior density becomes more smooth. This works roughly as follows.

Suppose that the model is defined by the system of ODEs $$ \dot{u}(t) = f(t, u(t), \theta)\,,\quad u(0) = u_0 $$ Fitting the solution of a system of ODEs through data can be hard, so why not replace the solution of the ODEs with something that can be fit through the data easily: for instance a B-spline. Obviously, this leads to the problem of over-fitting: when the number of knots equals the number of observations, the spline will fit the data perfectly. Also, we are not learning much about the parameters of the original model. We can solve both problems by penalizing. At each time point \(t\), the spline \(u\) has a total derivative \(\dot{u}(t)\), while according to the model, the total derivative should be equal to the vector field \(f(t, u(t), \theta)\). We can enforce that the spline resembles trajectories of the model by defining a penalty $$ \lambda \mathcal{S}[u] = \frac{\lambda}{2} \int_0^T \|\dot{u}(t) - f(t, u(t), \theta) \|^2 dt $$ which equals \(0\) exactly when \(u\) solves the system of ODEs. The log-likelihood of the data, given parameters \(\theta\) and spline \(u\) is then given by $$ \sum_{i=1}^n \log p(U_i | u(t_i), \theta) - \lambda \mathcal{S}[u]\,, $$ where \(p\) defines the measurement model (in our predator-prey model, \(p\) is the probability mass function of the Poisson distribution). When \(\lambda\) is close to \(0\), the spline is allowed to deviate from a true model trajectory, and fitting is easy. On the other hand, when \(\lambda\) is very large, the spline starts to resemble a true solution to the ODEs, and we will estimate \(\theta\) more precisely.

Stan implementation

In order to implement generalized profiling is Stan, we have to solve two problems. First, we have to construct a B-spline \(u\) in Stan, and compute the derivative \(\dot{u}\) of such a B-spline. Second, we have to numerically integrate the penalty \(\mathcal{S}[u]\). For the B-spline, I use an example from Milad Kharratzadeh, that uses a recursive Stan function to build a spline basis matrix in the generated quantities block. Milad gives a concise introduction to B-splines, which I will not repeat, but we do need the derivative of the spline.

Fortunately, we can define the derivative of a spline in terms of other B-splines. Define the spline basis of order \(k\) recursively $$ B_{i,k}(t) = \omega_{i,k} B_{i,k−1}(t) + (1−\omega_{i+1,k})B_{i+1,k−1}(t) $$ with coefficients \(\omega_{i, k} = (t - \tau_i) / (\tau_{i+k-1} - \tau_i)\) and knots \(\tau_1 \leq \tau_2 \leq \dots \leq \tau_m\). The base-case of the recursion is given by the order \(1\) splines $$ B_{i, 1}(t) = \left\{\begin{array}{ll} 1 & \mbox{if } \tau_i \leq t < \tau_{i+1} \\ 0 & \mbox{otherwise} \end{array}\right. $$ The derivative of a basis spline \(B\) is then given by $$ B_{i, k}'(t) = (k-1)\left(\alpha_{i, k} B_{i, k-1}(t) - \alpha_{i+1, k} B_{i+1, k-1}(t)\right) $$ where \(\alpha_{i, k} = 1/(\tau_{i+k-1} - \tau_i)\). We can prove this easily with induction.

The following Stan functions are implementations of B-splines and their derivative. The file splines.stan can be included in other Stan models with an #include "splines.stan" statement in the functions block.


Next, we need a way to compute the integral defined by \(\mathcal{S}[u]\). In general, this will not have a closed form expression, and therefore we use numerical integration. According to Simpson's rule, we can approximate the integral $$ \int_a^b g(x) dx = \tfrac{h}{3}\left(g(a) + 4 g(\tfrac12(b+a)) + g(b)\right) + \mathcal{O}(h^5) $$ where \(h = \tfrac12 (b-a)\). Hence, we will partition the interval \([0,T]\) into \(k-1\) sub-intervals of equal length \(2h = \frac{T}{k-1}\), and we have to know the value of the spline \(u(t)\) and it's derivative \(\dot{u}(t)\) at the \(2k-1\) end and midpoints of these intervals. The penalty functional \(\mathcal{S}[u]\) is then approximated with $$ \mathcal{S}[u] \approx \tfrac{h}{3} \sum_{i=1}^{k-1} \left(L(2(i-1)h) + 4 L((2i-1)h) + L(2ih)\right) $$ where \(L(t) = \tfrac12 \| \dot{u}(t) - f(t, u(t), \theta) \|^2 \). The number of "grid points" \(k\) is defined in the Stan model's data block as NumGridPts

The Stan model is organized as follows. In the functions block, we define the system of ODEs (copied directly from a previous post). Also, we define a convenient function seq to make sequences. In the data block, we import the observations and observation times, define the number of knots, grid points, the degree of the splines, the constant \(K\) and the weight of the penalty \(\lambda\). In the transformed data block, we define a knot vector and the grid for numerical integration. Then, we build the spline and spline derivative matrices BObs, BGrid, and DBGrid for the observation times and grid points. The parameters block declares the predator-prey model parameters \(a, b, c, d\), and the spline weights \(\upsilon\). In the model block, we compute the values of the spine \(u\) and spline derivative \(\dot{u}\) at the observation times (u = BObs * upsilon) and grid points (u_grid = BGrid * upsilon and du_grid = DBGrid * upsilon). These values are used for numerical integration of the penalty, and in the "sampling statement" of the Poisson-distributed observations.

Fitting the model to generated data

I will now demonstrate the Stan model with simulated data from the predator-prey model. We will use Python to generate data. First, we have to import some modules and compile the Stan model. A GitHub "gist" with all the python code in a single script is available here.

import pystan
import numpy as np
import scipy.stats as sts
import matplotlib.pyplot as plt
plt.rcParams.update({'font.size': 18})
from matplotlib.gridspec import GridSpec
from scipy.integrate import solve_ivp
import sdeint ## will be used later

## compile the Stan model
sm = pystan.StanModel(file="gen-prof-LV.stan")

Now, we define the predator-prey model and choose some parameters \(\theta = (a, b, c, d)\), and initial condition \(u_0 = (x_0, y_0)^T\). We also have to define the times we observe the system and the number of observations. Then we simulate the model using the solve_ivp method from scipy.integrate and generate noisy observations using poisson.rvs from scipy.stats.

## choose nice parameter values
a = 1.0
b = 0.4
c = 0.4
d = 0.5
theta = [a, b, c, d]

## observation times and initial conditions
NumObs = 25
tmin, tmax = 0, 50
TimesObs = np.linspace(tmin, tmax, NumObs)

## initial values
u0 = [1.0, 1.0] ## x0, y0
## the "system size" parameter K
K = 10

## define the Lotka-Volterra predator-prey model
def LV_sys(t, u):
    return [a*u[0] - b*u[0]*u[1], c*b*u[0]*u[1] - d*u[1]]

## use an ODE integrator to produce a trajectory
sol = solve_ivp(LV_sys, (tmin, tmax), u0, t_eval=TimesObs)
## generate random data (observations)
Obs = sts.poisson.rvs(sol.y.T*K)
## K determines the measurement noise

Next, we define a function run_gen_prof that makes the correct data dictionary for Stan and starts the Stan model. One of the arguments of the function is \(\lambda\), the weight of the penalty. We will run the Stan model twice. Once with a small \(\lambda = 1\), and once with a large \(\lambda = 100 \). The function run_gen_prof also returns the grid points used for numerical integration of the penalty term, that we will use for plotting the spline and it's derivative below.

def run_gen_prof(sm, obs, times, lam, system_size, deg=3, 
                 chains=4, chain_len=1000, thin=5):
    """
    convenient function to make a data dictionary for Stan
    and run the Stan model
    """
    n = len(times)
    ## put a knot at every observation and between two observations
    num_knots = 2*n-1
    ## number of points for numerical integration
    num_grid_pts = 3*num_knots-1
    grid_pts = np.linspace(times[0], times[n-1], num_grid_pts)
    data = {
        "NumKnots" : num_knots,
        "SplineDeg" : deg,
        "NumGridPts" : num_grid_pts,
        "NumObs" : n,
        "TimesObs" : times,
        "Obs" : obs,
        "K" : system_size,
        "Lambda" : lam,
    }
    settings = {
        "max_treedepth" : 15,
        "adapt_delta" : 0.9
    }
    sam = sm.sampling(data=data, chains=chains, iter=chain_len, 
                          control=settings, thin=thin)
    ## return the grid points for plotting
    return sam, grid_pts


## fit the model twice with different lambdas
lam_small = 1
sam_small, GridPts = run_gen_prof(sm, Obs, TimesObs, lam_small, K)
lam_large = 100
sam_large, _ = run_gen_prof(sm, Obs, TimesObs, lam_large, K)

In order to visualize the result, we define a function plot_gen_prof_fit that makes a plot of the data and fit. The function also plots the derivative of the spline \(\dot u\) and the vector field \(f(t, u(t), \theta)\), such that we can see how well the spline resembles a trajectory of the predator-prey model.

def plot_gen_prof_fit(sam, times, obs, grid_pts, system_size, n=None):
    """
    Make a figure with the data and the fitted spline.
    Also add the derivative of the spline and the vector field
    to give an indication of the deviation from the LV model
    """
    if n is None:
        n = len(times)
    chain_dict = sam.extract(permuted=True)
    fig = plt.figure(figsize=(14, 7))
    gs = GridSpec(4,1)
    ax = fig.add_subplot(gs[:2,0])
    bxs = [fig.add_subplot(gs[2,0], sharex=ax), 
           fig.add_subplot(gs[3,0], sharex=ax)]
    labels = ["Prey ($X$)", "Predator ($Y$)"]
    colors = ["tab:blue", "tab:orange"]
    pcts = [2.5, 97.5]
    ## make plots for predators and prey
    for i, color in enumerate(colors):
        ax.scatter(times[:n], obs[:n,i], color=color, edgecolors='k', 
                   zorder=3, label=labels[i])
        ## plot trajectories
        uss = chain_dict["uhat"][:,:,i].T
        mean_uhat = [system_size*np.mean(us) for us in uss]
        ax.plot(grid_pts, mean_uhat, color='k', zorder=2, 
                label='fit' if i == 0 else None)
        range_uhat = [system_size*np.percentile(us, pcts) for us in uss]
        ax.fill_between(grid_pts, *np.array(range_uhat).T, color=color, 
                        alpha=0.5, linewidth=0, zorder=1)
        ## plot simulations
        uss = chain_dict["usim"][:,:,i].T
        range_usim = [np.percentile(us, pcts) for us in uss]
        ax.fill_between(grid_pts, *np.array(range_usim).T, color=color, 
                        alpha=0.3, linewidth=0)
        ## plot derivative of the spline and the target derivative
        uss = chain_dict["duhat_real"][:,:,i].T
        mean_duhat_real = [system_size*np.mean(us) for us in uss]
        bxs[i].plot(grid_pts, mean_duhat_real, color=color, 
                    linewidth=3, label="spline")
        uss = chain_dict["duhat_target"][:,:,i].T
        mean_duhat_target = [system_size*np.mean(xs) for xs in uss]
        bxs[i].plot(grid_pts, mean_duhat_target, color='k', 
                    linestyle='--', label="LV model")
        bxs[i].legend(loc=1, ncol=2, prop={'size': 10})
    ## some labels etc...
    ax.legend(loc=1, ncol=3, prop={'size': 10})
    ax.set_ylabel("data and fit")
    for i, c in enumerate('xy'):
        bxs[i].set_ylabel(f"$\\frac{{d{c}}}{{dt}}$", 
                          rotation=0, va='center')
    ax.get_xaxis().set_visible(False)
    bxs[0].get_xaxis().set_visible(False)
    bxs[1].set_xlabel("Time ($t$)")
    fig.align_ylabels()
    return fig, (ax, *bxs)

Let us first have a look at the fit with \(\lambda = 1\).

fig, axs = plot_gen_prof_fit(sam_small, TimesObs, Obs, GridPts, K)
fig.savefig("gen-prof-fit-small-lambda.png", dpi=300, bbox_inches='tight')

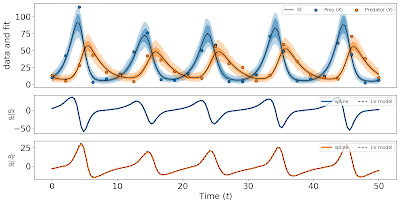
This is the result (click on the image to make it larger):

The scaled spline \(K u\) goes through almost all the data points \(X_i\) and \(Y_i\), and the derivative \(\dot{u}\) roughly follows the vector field \(f(t, u(t), \theta)\). However, the prediction intervals (dark colored bands) are quite wide, meaning that the uncertainty in \(u\) is very large between observations.

In order to make our spline-based model more closely related to the ODE model, we have to increase \(\lambda\). Now let us look at the fit with \(\lambda = 100\).

fig, axs = plot_gen_prof_fit(sam_large, TimesObs, Obs, GridPts, K)
fig.savefig("gen-prof-fit-large-lambda.png", dpi=300, bbox_inches='tight')

The result of taking \(\lambda\) large is that the spline \(K u\) no longer goes through all the data points \(X_i, Y_i\), as it should, since the the data is sampled from a Poisson distribution with mean \(K u(t_i) \). In addition, the derivative of the spline \(\dot{u}\) is now almost identical to the vector field \(f(t, u(t), \theta)\).

We will now look at the parameter estimates, and the effect of choosing small and large \(\lambda\). Again, we define a simple function plot_par_est to plot the estimates, and then use this function to create the two plots.

def plot_par_est(ax, sam, real_par_vals):
    """
    plot parameter estimates and compare them with the real values
    """
    chain_dict = sam.extract(permuted=True)
    parnames = ["a", "b", "c", "d"]
    latex_parnames = [f"${x}$" for x in parnames]
    pcts = [2.5, 97.5]

    ## plot estimates and 95 percentiles
    pos = range(len(parnames))
    means = [np.mean(chain_dict[x]) for x in parnames]
    ranges = [np.percentile(chain_dict[x], pcts) for x in parnames]
    ax.scatter(pos, [np.mean(chain_dict[x]) for x in parnames], 
               color='tab:red', label="estimate", marker='D', zorder=1)
    for p, r in zip(pos, ranges):
        ax.plot([p, p], r, color='tab:red', linewidth=2, zorder=1)
    
    ax.set_xticks(pos)
    ax.set_xticklabels(latex_parnames)

    ## plot real parameter values
    ax.scatter(pos, real_par_vals, color='k', label="real value", zorder=2)

    ax.legend(loc=1, ncol=1, prop={'size': 10})

    ax.set_ylabel("parameter value")
    ax.set_xlabel("parameter name")

## compare the parameter estimates with small and large lambda
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(7,3), sharey=True)
plot_par_est(ax1, sam_small, theta)
plot_par_est(ax2, sam_large, theta)

ax1.set_title(f"$\\lambda = {lam_small}$")
ax2.set_title(f"$\\lambda = {lam_large}$")

fig.savefig("gen-prof-estimates.png", dpi=300, bbox_inches='tight')

This results in the following figure.

The estimates (red diamonds) are pretty close to the real values (black dots) for both small and large \(\lambda\), but the 95% credibility intervals (CrI; the red vertical lines) are much smaller when \(\lambda = 100\).

disclaimer: I am not sure that these red lines are in fact 95% CrIs, as we are not fitting the true model to the data.

The question now is: what \(\lambda\) should we choose. In this case, the larger \(\lambda\) is, the better, because the spline gets closer to a trajectory of the model. However, as \(u\) is a B-spline, and not any differentiable function, we will never have \(\dot{u}(t) = f(t, u(u), \theta)\) for all but finitely many \(t\), and hence the penalty functional \(\mathcal{S}[u]\) will never be zero, unless the number of knots goes to infinity. In practice, one can try a number of increasing values for \(\lambda\) and choose different numbers of knots, and see when the estimates (and uncertainties) stabilize.

Model misspecification: the predator-prey model with intrinsic noise

An interesting benefit of the generalized profiling method over ODE integrators is that it can deal with some level of misspecification of the model. For biological systems, practically all models are misspecified. One source of misspecification is intrinsic noise, i.e., the true dynamics are not deterministic but stochastic. For the Lotka-Volterra predator-prey model, intrinsic noise has interesting consequences. The oscillatory dynamics predicted by the deterministic model have a fixed period and amplitude. When we add some noise to the system, we find that the model quickly gets out of phase with the deterministic trajectory, and that also the amplitude will vary over time. This makes it very difficult to use an ODE integrator to fit the model to data. We will see that the generalized profiling approach still does the job.

First, we will add diagonal multiplicative noise to the predator-prey model. We will use the sdeint module to simulate stochastic differential equations (SDEs). This module is still a pre-release, but it suffices for our purpose. Our stochastic predator-prey model is given by the SDEs $$ dx_t = (a x_t - bx_t y_t)dt + \sigma dW^1_t $$ $$ dy_t = (cb x_t y_t - d y_t)dt + \sigma dW^2_t $$ where \(W_t\) is a 2-dimensional Wiener process, and \(\sigma\) is the volatility. We use this model to generate data as follows

## add process noise to the model
sigma = 0.1
## other parameters stay the same

NumObs = 50
tmin, tmax = 0, 100
Thin = 10
TimesObsSDE = np.linspace(tmin, tmax, Thin*(NumObs-1)+1)
TimesObs = TimesObsSDE[::Thin]

## define the system
def LV_sys_drift(u, t):
    return np.array([a*u[0] - b*u[0]*u[1], c*b*u[0]*u[1] - d*u[1]])

def LV_sys_diffusion(u, t):
    return sigma * np.diag(u)

sol = sdeint.itoint(LV_sys_drift, LV_sys_diffusion, u0, TimesObsSDE)
sol_ode = solve_ivp(LV_sys, (tmin, tmax), u0, t_eval=TimesObsSDE)

## generate random data (observations)
Obs = sts.poisson.rvs(sol[::Thin,:]*K)

We then plot the trajectory and observations, and compare them to the trajectory predicted by the determinitic model.

## make a figure of the stochastic process, 
## the data and the deterministic skellaton
pcts = [2.5, 97.5] ## percentiles used later for CrIs
colors = ["tab:blue", "tab:orange"] ## color for prey and predator

fig, axs = plt.subplots(2, 1, figsize=(14, 7), sharex=True)

for i, color in enumerate(colors):
    axs[i].scatter(TimesObs, Obs[:,i], color=color, 
                   edgecolors='k', zorder=2, label='observations')
    axs[i].plot(TimesObsSDE, sol[:,i]*K, color=color,
                linewidth=3, zorder=1, label='stochastic process')
    axs[i].plot(TimesObsSDE, sol_ode.y[i]*K, color='k', alpha=0.75,
                label='deterministic skellaton')
    axs[i].legend(loc=0, ncol=3, prop={'size': 10})
    
axs[-1].set_xlabel("Time ($t$)")
axs[0].set_ylabel("$x$ SDE (blue)\n$x$ ODE (black)")
axs[1].set_ylabel("$y$ SDE (orange)\n$y$ ODE (black)")

fig.savefig("stochastic-LV-sim.png", dpi=300, bbox_inches='tight')

As mentioned, the stochastic trajectory gets out of phase with the deterministic model (black curves) and also the amplitude varies over time.

We now fit the same Stan model as before to the stochastic predator-prey data. We again use the run_gen_prof function to start the Stan program, and plot figures with the plot_gen_prof_fit and plot_par_est functions.

## choose a lambda, and fit the model...
lam = 10
sam, GridPts = run_gen_prof(sm, Obs, TimesObs, lam, K)

## plot the fit
fig, axs = plot_gen_prof_fit(sam, TimesObs, Obs, GridPts, K)
fig.savefig("gen-prof-fit-sde.png", dpi=300, bbox_inches='tight')
## plot estimates
fig, ax = plt.subplots(1, 1, figsize=(4,3))
plot_par_est(ax, sam, theta)
fig.savefig("gen-prof-estimates-sde.png", dpi=300, bbox_inches='tight')

The data and model fit are shown in the following figure. The generalized profiling fit stays close to the data, even though the stochastic path gets out of phase with the deterministic trajectory.

Also, the parameter estimates are still very close to the real values, as shown by the following figure

For this fit, I used a \(\lambda = 10\). Again, it is not clear what value for \(\lambda\) we should choose. In this case, a bigger \(\lambda\) is not necessarily better, as a finite \(\lambda\) allows the spline to deviate from the deterministic model, which is exactly what we need. In a follow-up paper Hooker et al. fit a model to a subset of the data and then compare model predictions with the left-out data points (i.e. forward cross-validation). This is repeated for different values of \(\lambda\) to determine the penalty weight yielding the best predictive performance. I experimented with this, but will leave it for a future blog post.

Theoretical considerations and further developments

The motivation for the penalty functional \(\mathcal{S}[u]\) may appear to be ad hoc, but in fact the justification for such a functional is given by some very interesting mathematics and physics. The theory of small random pertubations of dynamical systems developed by Friedlin and Wentzell tells us that the probability that a stochastic trajectory is "close" to the path \(u\) is roughly \(\exp(-\sigma^{-2} \mathcal{S}[u])\). Here the volatility \(\sigma\) should be very small and the noise is additive. Hence, in a way, the penalty (or action) functional \(\mathcal{S}[u]\) is proportional to the log-likelihood of the path \(u\).

There is no reason to choose B-splines for \(u\) other than convenience. In the so called tracking approach of Clairon and Brunel (2017), the path \(u(t)\) is instead defined in terms of a \(2n\) dimensional system of ODEs (where \(n\) is the dimension of the original system \(\dot{u} = f(t, u, \theta)\)). This system is derived as follows.

First, The discrete ubservations \(U_i\) at times \(0 \leq t_i \leq T\) are replaced by a continuous approximation \(U(t)\) with \(0\leq t\leq T\) (e.g. using a B-spline), and it is assumed that the measurment error is normally distributed with precision \(\kappa\). Hence, the log-likelihood of the smoothened data \(U(t)\) given trajectory \(u(t)\) is (up to a constant) equal to $$ -\frac{\kappa}{2}\int_0^T \| u(t) - U(t)\|^2 dt\,. $$ The penalty of a path \( u(t) \) is again given by $$ \frac{\lambda}{2}\int_0^T \| \dot{u}(t) - f(t, u(t), \theta)\|^2 dt\,. $$ Given a parameter \(\theta\), we now have to find a path \(u(t)\) with some initial condition \(u(0) = u_0\) that minimizes the action functional $$ \mathcal{S}[u] = \int_0^T \left(\frac{\kappa}{2} \| u(t) - U(t) \|^2 + \frac{\lambda}{2} \| \dot{u}(t) - f(t, u(t), \theta) \|^2 \right) dt\,. $$ This is a variational problem, and can be solved in terms of Hamilton's equations. First, we have to transform the Lagrangian (the integrand of the action functional) $$ \mathcal{L}(t, u, \dot{u}) = \frac{\kappa}{2} \| u(t) - U(t) \|^2 + \frac{\lambda}{2} \| \dot{u}(t) - f(t, u(t), \theta) \|^2 $$ into a Hamiltonian \(\mathcal{H}\). For this, we define the conjugate momentum $$ p = \frac{\partial \mathcal{L}}{\partial \dot{u}} = \lambda (\dot{u} - f(t, u, \theta))\,. $$ The Hamiltonian is then equal to $$ \mathcal{H}(t, u, p) = \langle \dot{u}, p \rangle - \mathcal{L}(t, u, \dot{u}) = \langle \lambda^{-1} p + f(t, u, \theta) , p \rangle - \frac{\kappa}{2} \|u-U\|^2 - \frac{\lambda^{-1}}{2} \|p\|^2 $$ which simplifies to $$ \mathcal{H}(t, u, p) = \frac{\lambda^{-1}}{2} \|p\|^2 + \langle f(t, u, \theta), p\rangle - \frac{\kappa}{2} \|u - U\|^2 $$ The path \(u\) that minimizes the action functional then has to satisfy Hamilton's equations: $$ \dot{u} = \frac{\partial \mathcal{H}}{\partial p} = f(t, u, \theta) + \lambda^{-1} p $$ and $$ \dot{p} = -\frac{\partial \mathcal{H}}{\partial u} = \kappa (u-U) - \left(\frac{\partial f}{\partial u}\right)^T p $$ together with the boundary conditions \(u(0) = u_0\) and \(p(T) = 0\). More details and a much more general derivation can be found in the paper by Clairon and Brunel. In a future blog post I want apply the tracking method to the predator-prey example.